On the Relaxation of Some Types of Dirichlet Minimum Problems for Unbounded Functionals
Abstract
In this paper, considered a Borel function g on 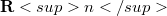 taking its values in
taking its values in ![[0,+∈fty]](https://358864.dpsou.asia/plugins/generic/latexRender/cache/58a7e463b0398b5e001377bb1bf80ce4.png) , verifying some weak hypothesis of continuity, such that
, verifying some weak hypothesis of continuity, such that 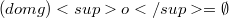 and
and 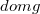 is convex, we obtain an integral representation result for the lower semicontinuous envelope in the
is convex, we obtain an integral representation result for the lower semicontinuous envelope in the 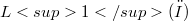 - topology of the integral functional
- topology of the integral functional 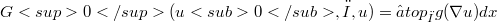 , where(Error rendering LaTeX formula) only on suitable pin is of the boundary of
, where(Error rendering LaTeX formula) only on suitable pin is of the boundary of 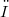 that lie, for example, on affine spaces orthogonal to
that lie, for example, on affine spaces orthogonal to 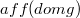 , for boundary values
, for boundary values 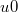 satisfying suitable compatibility conditions and
satisfying suitable compatibility conditions and 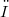 is geometrically well situated respect to
is geometrically well situated respect to 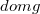 . Then we apply this result to Dirichlet nunimum problems.
. Then we apply this result to Dirichlet nunimum problems.
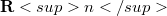 taking its values in
taking its values in ![[0,+∈fty]](https://358864.dpsou.asia/plugins/generic/latexRender/cache/58a7e463b0398b5e001377bb1bf80ce4.png) , verifying some weak hypothesis of continuity, such that
, verifying some weak hypothesis of continuity, such that 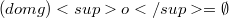 and
and 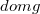 is convex, we obtain an integral representation result for the lower semicontinuous envelope in the
is convex, we obtain an integral representation result for the lower semicontinuous envelope in the 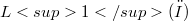 - topology of the integral functional
- topology of the integral functional 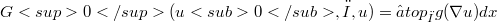 , where(Error rendering LaTeX formula) only on suitable pin is of the boundary of
, where(Error rendering LaTeX formula) only on suitable pin is of the boundary of 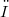 that lie, for example, on affine spaces orthogonal to
that lie, for example, on affine spaces orthogonal to 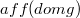 , for boundary values
, for boundary values 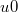 satisfying suitable compatibility conditions and
satisfying suitable compatibility conditions and 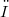 is geometrically well situated respect to
is geometrically well situated respect to 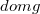 . Then we apply this result to Dirichlet nunimum problems.
. Then we apply this result to Dirichlet nunimum problems.DOI Code:
10.1285/i15900932v19n2p231
Classification:
49J45
Full Text: PDF


