On Defining the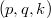 
-Generalized Gamma Function
Abstract
In this paper, we introduce a 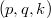-generalization of the gamma function and investigate some basic identities and properties. Further, we define a 
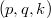-integral representation for this function. As an application, we give some double inequalities concerning the -generalized gamma function by using of its -integral representation.
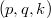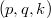-generalization of the gamma function and investigate some basic identities and properties. Further, we define a -integral representation for this function. As an application, we give some double inequalities concerning the -generalized gamma function by using of its -integral representation.DOI Code:
10.1285/i15900932v39n1p107
Keywords:
Gamma function; $q$-integral; $(p,q,k)$-generalized gamma function; $(p,q,k)$-generalized Pocchammer symbol; inequality
Full Text: PDF
