Congruences for (2, 3)-regular partition with designated summands
Abstract
Let 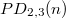 count the number of partitions of
count the number of partitions of 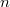 with designated summands in which parts are not multiples of
with designated summands in which parts are not multiples of 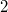 or
or 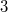 . In this work, we establish congruences modulo powers of 2 and 3 for
. In this work, we establish congruences modulo powers of 2 and 3 for 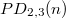 . For example, for each \quad
. For example, for each \quad 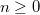 and
and 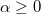 \quad
\quad 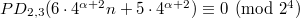 and
and 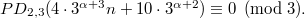
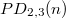 count the number of partitions of
count the number of partitions of 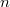 with designated summands in which parts are not multiples of
with designated summands in which parts are not multiples of 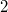 or
or 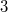 . In this work, we establish congruences modulo powers of 2 and 3 for
. In this work, we establish congruences modulo powers of 2 and 3 for 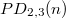 . For example, for each \quad
. For example, for each \quad 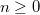 and
and 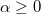 \quad
\quad 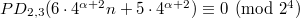 and
and 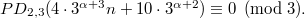
DOI Code:
10.1285/i15900932v36n2p99
Keywords:
Designated summands; Congruences; Theta functions; Dissections
Full Text: PDF


