A Quantitative Characterization of Some Finite Simple Groups Through Order and Degree Pattern
Abstract
Let 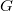 be a finite group with
be a finite group with  , where
, where  are prime numbers and
are prime numbers and  are natural numbers. The prime graph
are natural numbers. The prime graph  of
of 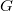 is a simple graph whose vertex set is
is a simple graph whose vertex set is  and two distinct primes
and two distinct primes  and
and  are joined by an edge if and only if
are joined by an edge if and only if 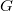 has an element of order
has an element of order  . The degree
. The degree  of a vertex
of a vertex  is the number of edges incident on
is the number of edges incident on  , and the
, and the  -tuple
-tuple  is called the degree pattern of
is called the degree pattern of 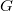 . We say that the problem of OD-characterization is solved for a finite group
. We say that the problem of OD-characterization is solved for a finite group 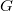 if we determine the number of pairwise non-isomorphic finite groups with the same order and degree pattern as
if we determine the number of pairwise non-isomorphic finite groups with the same order and degree pattern as 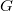 . The purpose of this paper is twofold. First, it completely solves the OD-characterization problem for every finite non-Abelian simple groups their orders having prime divisors at most 17. Second, it provides a list of finite (simple) groups for which the problem of OD-characterization have been already solved.
. The purpose of this paper is twofold. First, it completely solves the OD-characterization problem for every finite non-Abelian simple groups their orders having prime divisors at most 17. Second, it provides a list of finite (simple) groups for which the problem of OD-characterization have been already solved.
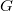 be a finite group with
be a finite group with  , where
, where  are prime numbers and
are prime numbers and  are natural numbers. The prime graph
are natural numbers. The prime graph  of
of 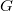 is a simple graph whose vertex set is
is a simple graph whose vertex set is  and two distinct primes
and two distinct primes  and
and  are joined by an edge if and only if
are joined by an edge if and only if 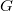 has an element of order
has an element of order  . The degree
. The degree  of a vertex
of a vertex  is the number of edges incident on
is the number of edges incident on  , and the
, and the  -tuple
-tuple  is called the degree pattern of
is called the degree pattern of 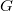 . We say that the problem of OD-characterization is solved for a finite group
. We say that the problem of OD-characterization is solved for a finite group 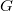 if we determine the number of pairwise non-isomorphic finite groups with the same order and degree pattern as
if we determine the number of pairwise non-isomorphic finite groups with the same order and degree pattern as 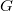 . The purpose of this paper is twofold. First, it completely solves the OD-characterization problem for every finite non-Abelian simple groups their orders having prime divisors at most 17. Second, it provides a list of finite (simple) groups for which the problem of OD-characterization have been already solved.
. The purpose of this paper is twofold. First, it completely solves the OD-characterization problem for every finite non-Abelian simple groups their orders having prime divisors at most 17. Second, it provides a list of finite (simple) groups for which the problem of OD-characterization have been already solved.DOI Code:
10.1285/i15900932v34n2p91
Keywords:
Prime graph; degree pattern; OD-characterization
Full Text: PDF


