Large quartic groups on translation planes, I --odd order: Characterization of the Hering planes
Abstract
The Hering planes of order 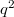 and the Walker planes of order
and the Walker planes of order 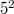 are shown to be the unique classes of planes with spreads in
are shown to be the unique classes of planes with spreads in  or
or 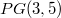 , respectively, admitting at least two 'large' quartic groups with distinct centers.
, respectively, admitting at least two 'large' quartic groups with distinct centers.
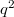 and the Walker planes of order
and the Walker planes of order 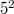 are shown to be the unique classes of planes with spreads in
are shown to be the unique classes of planes with spreads in  or
or 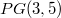 , respectively, admitting at least two 'large' quartic groups with distinct centers.
, respectively, admitting at least two 'large' quartic groups with distinct centers.DOI Code:
10.1285/i15900932v23n1p151
Keywords:
Quartic group; Translation plane; Hering plane
Classification:
51E23; 51A40
Full Text: PDF


