Some sporadic translation planes of order 
Abstract
In \cite{PK}, the authors constructed a translation plane  of order
of order  arising from replacement of a sporadic chain
arising from replacement of a sporadic chain  of reguli in a regular spread
of reguli in a regular spread 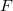 of
of 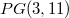 . They also showed that two more non isomorphic translation planes, called
. They also showed that two more non isomorphic translation planes, called 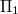 and
and 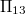 , arise respectively by derivation and double derivation in
, arise respectively by derivation and double derivation in 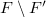 which correspond to a further replacement of a regulus with its opposite regulus and a pair of reguli with their opposite reguli, respectively. In \cite{AL}, the authors proved that the translation complement of
which correspond to a further replacement of a regulus with its opposite regulus and a pair of reguli with their opposite reguli, respectively. In \cite{AL}, the authors proved that the translation complement of  contains a subgroup isomorphic to
contains a subgroup isomorphic to 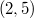 . Here, the full collineation group of each of the planes
. Here, the full collineation group of each of the planes  ,
, 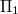 and
and 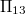 is determined.
is determined.
 of order
of order  arising from replacement of a sporadic chain
arising from replacement of a sporadic chain  of reguli in a regular spread
of reguli in a regular spread 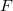 of
of 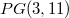 . They also showed that two more non isomorphic translation planes, called
. They also showed that two more non isomorphic translation planes, called 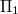 and
and 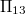 , arise respectively by derivation and double derivation in
, arise respectively by derivation and double derivation in 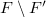 which correspond to a further replacement of a regulus with its opposite regulus and a pair of reguli with their opposite reguli, respectively. In \cite{AL}, the authors proved that the translation complement of
which correspond to a further replacement of a regulus with its opposite regulus and a pair of reguli with their opposite reguli, respectively. In \cite{AL}, the authors proved that the translation complement of  contains a subgroup isomorphic to
contains a subgroup isomorphic to 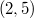 . Here, the full collineation group of each of the planes
. Here, the full collineation group of each of the planes  ,
, 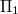 and
and 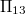 is determined.
is determined.DOI Code:
10.1285/i15900932v29n1supplp121
Keywords:
Translation plane; Replacement; Collineation; Chain of circles
Translation plane; Replacement; Collineation; Chain of circles
Full Text: PDF


