Introduction
Abstract
En
A characterization of v-irreducible elements and of strongly v-irriducible elements of a distributive lattice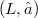
was given by D.Drake and W.J.Thorn in (1).Among other things in (1)it was proven that an element 
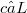is v-irreducible if one can identify 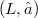, by means of a lattice isomorphism f, with a sublattice 
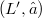of the power set 
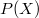of a suitable set X, in such a way that 
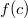is the closure in 
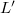of an element 
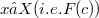is the minimum element in 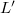,with respect to the set inclusion, including x).
As is well-known an element of a distributive lattice is v-irreducible iff it is v-prime.This property is exploited is an essential manner in (1).Now then in our paper we took this property as a starting point for a characterization cf v-prime and of strongly v-prime elements of any partially ordered set (in particular of any lattice).Here,on the analogy of some characterization of v-prime elements and of strongly v-prime elements of a lattice, an element c of a partially ordered set(shortly "poset" 
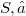) is said v-prime if the subset 
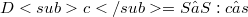is v-directed, i.e. 
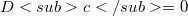or for every 
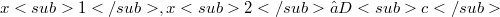(for every(Error rendering LaTeX formula))there exists 
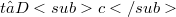such that 
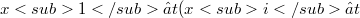for every 
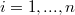); moreover c is said strongly v-prime if 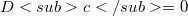or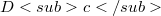 
has maxium element.Then we prove than an element 
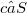is v-prime in 
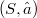if we can identify 
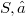by means of an order isomorphism f,with a set (but not necessarily a lattice) of sets of the type of (1) in such a way that 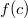is the closure in 
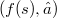of a element of 
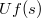;moreover we prove that c is strongly v-prime in 
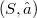if for all function f of the above type the set 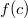is the closure in 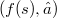of an element of .
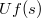It
D.Drake e W.J.Thorn hanno in (1)una caratterizzazione degli elementi v-irriducibili e degli elementi fortemente v-irriducubili di un reticolo distributivo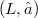.tra l'altro in (1)è stato provato che un elemento 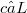è irriducibile se e solo se si può identificare 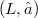,tramite un isomorfismo reticolare f,con un sottoreticolo 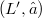del reticolo delle parti 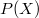di un opportuno insieme X in tal modo che 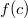è la chiusura di 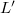di un certo elemento 
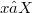(cioè 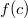è il più piccolo elemento di 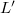,rispetto all'inclusione insiemistica, cui appartiene x).Come è ben noto un elemento di un reticolo distributivo è v-irriducibile se e solo se esso è v-primo.Questa propietà è usata in maniera essenziale in (1).In questo lavoro noi prendiamo lo spunto da questa propietà per dare una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un qualsiasi insieme parzialmente ordinato(in particolare di qualsiasi reticolo 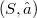). Precisiamo che quì, in analogia con una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un reticolo,un elemto c di un insieme parzialmente ordinato ( 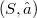è detto v-primo se il sottoinsieme 
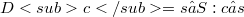è v-diretto, cioè 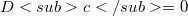oppure per ogni 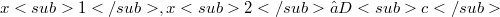per ogni(Error rendering LaTeX formula))esiste 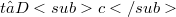tale ch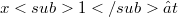e 
e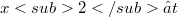 
(
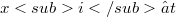per ogni 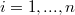);inoltre c è detto fortemente v-primo se 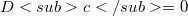oppure 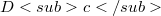è dotato di massimo.Allora noi proviamo che un elemento 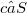è v-primo in 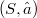se e solo se possiamo identificare 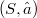, tramite un isomorfismo f rispetto all'ordinamento, con un insieme di insiemi(non necessariamente un reticolo di insiemi) del tipo (1) in modo tale che 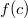è la chiusura in (
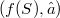di un elemento di 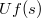);inoltre proviamo che c è fortemente v-primo in 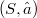se e solo se per ogni isomorfismo f del tipo su menzionato l'insieme 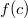è la chiusura in 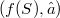di un punto di .
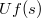A characterization of v-irreducible elements and of strongly v-irriducible elements of a distributive lattice
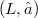was given by D.Drake and W.J.Thorn in (1).Among other things in (1)it was proven that an element 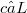is v-irreducible if one can identify 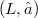, by means of a lattice isomorphism f, with a sublattice 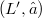of the power set 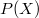of a suitable set X, in such a way that 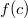is the closure in 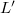of an element 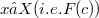is the minimum element in 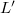,with respect to the set inclusion, including x).
As is well-known an element of a distributive lattice is v-irreducible iff it is v-prime.This property is exploited is an essential manner in (1).Now then in our paper we took this property as a starting point for a characterization cf v-prime and of strongly v-prime elements of any partially ordered set (in particular of any lattice).Here,on the analogy of some characterization of v-prime elements and of strongly v-prime elements of a lattice, an element c of a partially ordered set(shortly "poset" ) 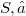is said v-prime if the subset 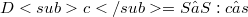is v-directed, i.e. 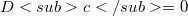or for every 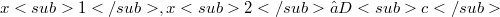(for every(Error rendering LaTeX formula))there exists 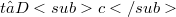such that 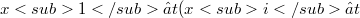for every 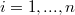); moreover c is said strongly v-prime if 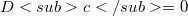or 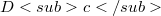has maxium element.Then we prove than an element 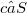is v-prime in 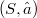if we can identify 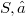by means of an order isomorphism f,with a set (but not necessarily a lattice) of sets of the type of (1) in such a way that 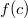is the closure in 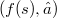of a element of 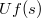;moreover we prove that c is strongly v-prime in 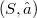if for all function f of the above type the set 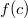is the closure in 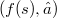of an element of 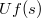.It
D.Drake e W.J.Thorn hanno in (1)una caratterizzazione degli elementi v-irriducibili e degli elementi fortemente v-irriducubili di un reticolo distributivo
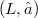.tra l'altro in (1)è stato provato che un elemento 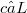è irriducibile se e solo se si può identificare 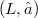,tramite un isomorfismo reticolare f,con un sottoreticolo 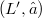del reticolo delle parti 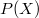di un opportuno insieme X in tal modo che 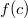è la chiusura di 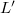di un certo elemento 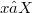(cioè 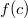è il più piccolo elemento di 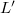,rispetto all'inclusione insiemistica, cui appartiene x).Come è ben noto un elemento di un reticolo distributivo è v-irriducibile se e solo se esso è v-primo.Questa propietà è usata in maniera essenziale in (1).In questo lavoro noi prendiamo lo spunto da questa propietà per dare una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un qualsiasi insieme parzialmente ordinato(in particolare di qualsiasi reticolo 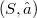). Precisiamo che quì, in analogia con una caratterizzazione degli elementi v-primi e degli elementi fortemente v-primi di un reticolo,un elemto c di un insieme parzialmente ordinato ( 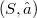è detto v-primo se il sottoinsieme 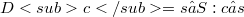è v-diretto, cioè 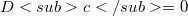oppure per ogni 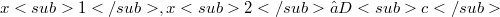per ogni(Error rendering LaTeX formula))esiste 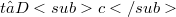tale ch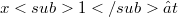e e 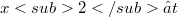( 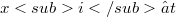per ogni 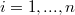);inoltre c è detto fortemente v-primo se 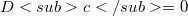oppure 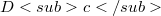è dotato di massimo.Allora noi proviamo che un elemento 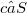è v-primo in 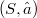se e solo se possiamo identificare 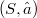, tramite un isomorfismo f rispetto all'ordinamento, con un insieme di insiemi(non necessariamente un reticolo di insiemi) del tipo (1) in modo tale che 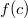è la chiusura in ( 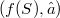di un elemento di 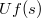);inoltre proviamo che c è fortemente v-primo in 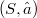se e solo se per ogni isomorfismo f del tipo su menzionato l'insieme 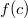è la chiusura in 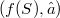di un punto di 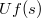.DOI Code:
�
Full Text: PDF
