A strong barrelledness property for space 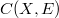
Abstract
A locally convex space (lcs) E is called s-barrelled [DiK] if every sequentially closed linear map,i.e. with sequentially closed graph, of E into a Fréchet space,i.e. a metrizable and complete lcs, is continuous. Let E be a lcs, X a locally compact topological space, 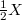 its Stone-Cech compactification. If
its Stone-Cech compactification. If 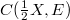 is s-barrelled, then
is s-barrelled, then 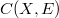 is s-barrelled iff X is realcompact, where all spaces of continuous functions are provided with the compact-open topology. Some remarks and corollaries are also included.
is s-barrelled iff X is realcompact, where all spaces of continuous functions are provided with the compact-open topology. Some remarks and corollaries are also included.
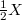 its Stone-Cech compactification. If
its Stone-Cech compactification. If 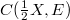 is s-barrelled, then
is s-barrelled, then 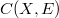 is s-barrelled iff X is realcompact, where all spaces of continuous functions are provided with the compact-open topology. Some remarks and corollaries are also included.
is s-barrelled iff X is realcompact, where all spaces of continuous functions are provided with the compact-open topology. Some remarks and corollaries are also included.DOI Code:
10.1285/i15900932v14n2p199
Full Text: PDF


