On Mallios 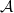 -connections as connections on principal sheaves
-connections as connections on principal sheaves
Abstract
Motivated by [5], we associate a vector sheaf  with a principal sheaf
with a principal sheaf 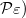 , called sheaf of frames of
, called sheaf of frames of  . We show that
. We show that 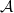 -connections on
-connections on  correspond to connections on
correspond to connections on 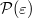 . The latter are defined by an appropriate family of local matrices or, equivalently, by a morphism acting on
. The latter are defined by an appropriate family of local matrices or, equivalently, by a morphism acting on 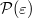 , analogously to the operator of an \mathcal A$-collection.
, analogously to the operator of an \mathcal A$-collection.
 with a principal sheaf
with a principal sheaf 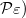 , called sheaf of frames of
, called sheaf of frames of  . We show that
. We show that 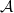 -connections on
-connections on  correspond to connections on
correspond to connections on 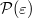 . The latter are defined by an appropriate family of local matrices or, equivalently, by a morphism acting on
. The latter are defined by an appropriate family of local matrices or, equivalently, by a morphism acting on 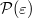 , analogously to the operator of an \mathcal A$-collection.
, analogously to the operator of an \mathcal A$-collection.DOI Code:
10.1285/i15900932v14n2p237
Full Text: PDF


