On Rund's connection
Abstract
We show that the holomorphic curvature 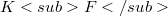 (associated with a complex Finsler metric F)in the sense of M. Suzuki, [13] ,and B. Wong,[15], is (in the smooth case) precisely the holomorphic curvature of a connection essentially due to H. Rund, [12] (and reproposed in the bundle-theoretic setting by S. Kobayashi, [8]). We prove a complex analogue of Deike's theorem in real Finsler geometry. The indicatrix in each fibre of a convex complex Finsler bundle is shown to be an extrinsic sphere.
(associated with a complex Finsler metric F)in the sense of M. Suzuki, [13] ,and B. Wong,[15], is (in the smooth case) precisely the holomorphic curvature of a connection essentially due to H. Rund, [12] (and reproposed in the bundle-theoretic setting by S. Kobayashi, [8]). We prove a complex analogue of Deike's theorem in real Finsler geometry. The indicatrix in each fibre of a convex complex Finsler bundle is shown to be an extrinsic sphere.
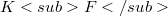 (associated with a complex Finsler metric F)in the sense of M. Suzuki, [13] ,and B. Wong,[15], is (in the smooth case) precisely the holomorphic curvature of a connection essentially due to H. Rund, [12] (and reproposed in the bundle-theoretic setting by S. Kobayashi, [8]). We prove a complex analogue of Deike's theorem in real Finsler geometry. The indicatrix in each fibre of a convex complex Finsler bundle is shown to be an extrinsic sphere.
(associated with a complex Finsler metric F)in the sense of M. Suzuki, [13] ,and B. Wong,[15], is (in the smooth case) precisely the holomorphic curvature of a connection essentially due to H. Rund, [12] (and reproposed in the bundle-theoretic setting by S. Kobayashi, [8]). We prove a complex analogue of Deike's theorem in real Finsler geometry. The indicatrix in each fibre of a convex complex Finsler bundle is shown to be an extrinsic sphere.DOI Code:
10.1285/i15900932v15n1p85
Classification:
51H10; 51H20; 51A35
Full Text: PDF


