Some geometric estimates of the first eigenvalue of quasilinear and 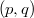 -Laplace operators
-Laplace operators
Abstract
In this paper, we use a particular smooth function 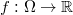 on a bounded domain
on a bounded domain  of a Riemannian manifold
of a Riemannian manifold 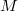 to estimate the lower bound of the first eigenvalue for quasilinear operator
to estimate the lower bound of the first eigenvalue for quasilinear operator 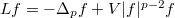 . In this way, we also present a lower bound for the first eigenvalue of the
. In this way, we also present a lower bound for the first eigenvalue of the 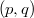 -Laplacian on compact manifolds.
-Laplacian on compact manifolds.
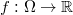 on a bounded domain
on a bounded domain  of a Riemannian manifold
of a Riemannian manifold 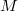 to estimate the lower bound of the first eigenvalue for quasilinear operator
to estimate the lower bound of the first eigenvalue for quasilinear operator 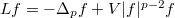 . In this way, we also present a lower bound for the first eigenvalue of the
. In this way, we also present a lower bound for the first eigenvalue of the 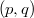 -Laplacian on compact manifolds.
-Laplacian on compact manifolds.DOI Code:
10.1285/i15900932v44n2p45
Keywords:
(p,q)-Laplacian; quasilinear operator; first eigenvalue
Full Text: PDF


