Minimal Hopf-Galois Structures on Separable Field Extensions
Abstract
In Hopf-Galois theory, every 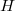 -Hopf-Galois structure on a field extension
-Hopf-Galois structure on a field extension 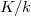 gives rise to an injective map
gives rise to an injective map 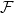 from the set of
from the set of 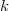 -sub-Hopf algebras of
-sub-Hopf algebras of 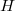 into the intermediate fields of
into the intermediate fields of 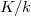 . Recent papers on the failure of the surjectivity of
. Recent papers on the failure of the surjectivity of 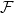 reveal that there exist many Hopf-Galois structures for which there are many more subfields than sub-Hopf algebras. In this paper we survey and illustrate group-theoretical methods to determine
reveal that there exist many Hopf-Galois structures for which there are many more subfields than sub-Hopf algebras. In this paper we survey and illustrate group-theoretical methods to determine 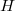 -Hopf-Galois structures on finite separable extensions in the extreme situation when
-Hopf-Galois structures on finite separable extensions in the extreme situation when 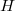 has only two sub-Hopf algebras. This corresponds to the case when the lack of surjectivity is at its extreme.
has only two sub-Hopf algebras. This corresponds to the case when the lack of surjectivity is at its extreme.
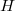 -Hopf-Galois structure on a field extension
-Hopf-Galois structure on a field extension 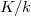 gives rise to an injective map
gives rise to an injective map 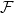 from the set of
from the set of 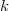 -sub-Hopf algebras of
-sub-Hopf algebras of 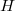 into the intermediate fields of
into the intermediate fields of 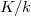 . Recent papers on the failure of the surjectivity of
. Recent papers on the failure of the surjectivity of 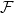 reveal that there exist many Hopf-Galois structures for which there are many more subfields than sub-Hopf algebras. In this paper we survey and illustrate group-theoretical methods to determine
reveal that there exist many Hopf-Galois structures for which there are many more subfields than sub-Hopf algebras. In this paper we survey and illustrate group-theoretical methods to determine 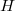 -Hopf-Galois structures on finite separable extensions in the extreme situation when
-Hopf-Galois structures on finite separable extensions in the extreme situation when 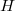 has only two sub-Hopf algebras. This corresponds to the case when the lack of surjectivity is at its extreme.
has only two sub-Hopf algebras. This corresponds to the case when the lack of surjectivity is at its extreme.DOI Code:
10.1285/i15900932v41n1p55
Keywords:
Galois and Hopf-Galois field extensions; Galois correspondence; characteristically simple groups
Full Text: PDF


