Biharmonic Hermitian vector bundles over compact Kähler manifolds and compact Einstein Riemannian manifolds
Abstract
We show, for every Hermitian vector bundle 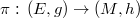 over a compact Kähler Einstein manifold
over a compact Kähler Einstein manifold 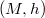 , if the projection
, if the projection 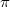 is biharmonic, then it is harmonic. On a biharmonic Hermitian vector bundle over a compact Riemannian manifold with positive Ricci curvature, we show a new estimate of the first eigenvalue of the Laplacian.
is biharmonic, then it is harmonic. On a biharmonic Hermitian vector bundle over a compact Riemannian manifold with positive Ricci curvature, we show a new estimate of the first eigenvalue of the Laplacian.
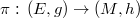 over a compact Kähler Einstein manifold
over a compact Kähler Einstein manifold 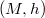 , if the projection
, if the projection  is biharmonic, then it is harmonic. On a biharmonic Hermitian vector bundle over a compact Riemannian manifold with positive Ricci curvature, we show a new estimate of the first eigenvalue of the Laplacian.
is biharmonic, then it is harmonic. On a biharmonic Hermitian vector bundle over a compact Riemannian manifold with positive Ricci curvature, we show a new estimate of the first eigenvalue of the Laplacian.DOI Code:
10.1285/i15900932v39n2p95
Keywords:
biharmonic maps; harmonic maps; Kähler Einstein manifolds; Hermitian vector bundles
Full Text: PDF


