On the ranks of homogeneous polynomials of degree at least 9 and border rank 5
Abstract
Let 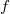 be a degree
be a degree 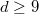 homogenous polynomial with border rank
homogenous polynomial with border rank 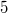 . We prove that it has rank at most
. We prove that it has rank at most 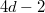 and give better results when
and give better results when 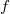 essentially depends on at most
essentially depends on at most 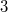 variables or there are other conditions on the scheme evincing the cactus and border rank of
variables or there are other conditions on the scheme evincing the cactus and border rank of 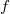 . We always assume that
. We always assume that 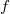 essentially depends on at most
essentially depends on at most 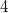 variables, because the other case was done by myself in Acta Math. Vietnam. 42 (2017), 509-531.
variables, because the other case was done by myself in Acta Math. Vietnam. 42 (2017), 509-531.
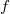 be a degree
be a degree 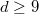 homogenous polynomial with border rank
homogenous polynomial with border rank 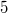 . We prove that it has rank at most
. We prove that it has rank at most 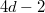 and give better results when
and give better results when 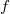 essentially depends on at most
essentially depends on at most 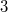 variables or there are other conditions on the scheme evincing the cactus and border rank of
variables or there are other conditions on the scheme evincing the cactus and border rank of 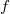 . We always assume that
. We always assume that 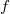 essentially depends on at most
essentially depends on at most 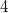 variables, because the other case was done by myself in Acta Math. Vietnam. 42 (2017), 509-531.
variables, because the other case was done by myself in Acta Math. Vietnam. 42 (2017), 509-531.DOI Code:
10.1285/i15900932v38n2p55
Keywords:
symmetric tensor rank; border rank; cactus rank
Full Text: PDF


