A note on groups with restrictions on centralizers of in nite index
Abstract
A group 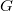 is said to be an {\it
is said to be an {\it 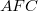 -group} if for each element
-group} if for each element  of
of 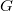 , either
, either  has finitely many conjugates or the factor group
has finitely many conjugates or the factor group 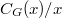 is finite. In this survey article some results concerning
is finite. In this survey article some results concerning 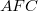 -groups and minimal-non-
-groups and minimal-non-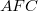 groups are collected
groups are collected
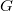 is said to be an {\it
is said to be an {\it 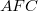 -group} if for each element
-group} if for each element  of
of 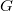 , either
, either  has finitely many conjugates or the factor group
has finitely many conjugates or the factor group 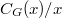 is finite. In this survey article some results concerning
is finite. In this survey article some results concerning 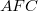 -groups and minimal-non-
-groups and minimal-non-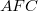 groups are collected
groups are collectedDOI Code:
10.1285/i15900932v36suppl1p1
Keywords:
$AFC$-group; minimal-non-$AFC$ group; $FC$-centre
Full Text: PDF


