On derivable Baer-elation planes
Abstract
In [5], Jha and Johnson introduce Baer-elation planes. These are finite translation planes of order 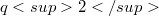 ,
, 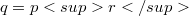 which admit both Baer p-collineation groups and elation groups which normalize each other.By a result of Foulser [3],
which admit both Baer p-collineation groups and elation groups which normalize each other.By a result of Foulser [3], 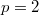 .Jha-Johnson consider, in particular, Baer-elation planes of order
.Jha-Johnson consider, in particular, Baer-elation planes of order 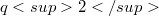 with kernel
with kernel 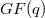 of type (2,q) or type (q,2). That is, there is a Baer or elation group of order q.By the incompatibility results of Jha-Johnson [7], [8], the corresponding or Baer group has order
of type (2,q) or type (q,2). That is, there is a Baer or elation group of order q.By the incompatibility results of Jha-Johnson [7], [8], the corresponding or Baer group has order 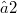 .
.
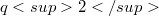 ,
, 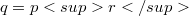 which admit both Baer p-collineation groups and elation groups which normalize each other.By a result of Foulser [3],
which admit both Baer p-collineation groups and elation groups which normalize each other.By a result of Foulser [3], 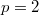 .Jha-Johnson consider, in particular, Baer-elation planes of order
.Jha-Johnson consider, in particular, Baer-elation planes of order 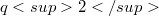 with kernel
with kernel 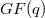 of type (2,q) or type (q,2). That is, there is a Baer or elation group of order q.By the incompatibility results of Jha-Johnson [7], [8], the corresponding or Baer group has order
of type (2,q) or type (q,2). That is, there is a Baer or elation group of order q.By the incompatibility results of Jha-Johnson [7], [8], the corresponding or Baer group has order 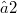 .
.DOI Code:
10.1285/i15900932v7n1p19
Full Text: PDF


