Almost conformal 2-cosymplectic pseudo-Sasakian manifolds
Abstract
In the last years several papers have been concerned with almost r-contact or r-paracontact manifolds (see [6] and [14]). On the other hand, V.V. Goldberg and R. Rosta have recently studied in [12] almost 1-contact pseudo-Riemannian manifolds which are endowed with a conformal cosymplectic pseudo-Sasakian structure. Since the manifolds M which we are going to discuss are connected and paracompact,we denote by 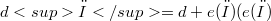 : exterior product by the closed 1-form
: exterior product by the closed 1-form 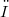 ) the cohomology operator (see [13]) on M. Then any form
) the cohomology operator (see [13]) on M. Then any form 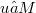 such that
such that 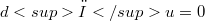 is said to be
is said to be 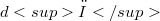 -closed. The present paper is devoted to the study of even dimensional pseudo Riemannian manifolds of signature
-closed. The present paper is devoted to the study of even dimensional pseudo Riemannian manifolds of signature 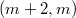 which are endowed with an almost conformal 2-cosymplectic pseudo-Sasakian structure. Such a manifold is denoted by
which are endowed with an almost conformal 2-cosymplectic pseudo-Sasakian structure. Such a manifold is denoted by 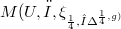 , and its structure tensor fields
, and its structure tensor fields 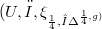 are: the paracomplex operator (see [15]), an exterior recurrent (see [9]) 2-form of rank
are: the paracomplex operator (see [15]), an exterior recurrent (see [9]) 2-form of rank 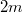 , two structure vector fields
, two structure vector fields 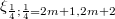 , two structure 1-forms
, two structure 1-forms 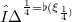
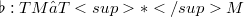 is the musical isomorphism [6] defined by g) and the pseudo-Riemannian tensor g of M respectively.
is the musical isomorphism [6] defined by g) and the pseudo-Riemannian tensor g of M respectively.
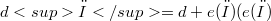 : exterior product by the closed 1-form
: exterior product by the closed 1-form 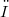 ) the cohomology operator (see [13]) on M. Then any form
) the cohomology operator (see [13]) on M. Then any form 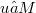 such that
such that 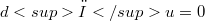 is said to be
is said to be 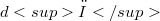 -closed. The present paper is devoted to the study of even dimensional pseudo Riemannian manifolds of signature
-closed. The present paper is devoted to the study of even dimensional pseudo Riemannian manifolds of signature 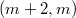 which are endowed with an almost conformal 2-cosymplectic pseudo-Sasakian structure. Such a manifold is denoted by
which are endowed with an almost conformal 2-cosymplectic pseudo-Sasakian structure. Such a manifold is denoted by 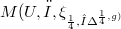 , and its structure tensor fields
, and its structure tensor fields 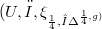 are: the paracomplex operator (see [15]), an exterior recurrent (see [9]) 2-form of rank
are: the paracomplex operator (see [15]), an exterior recurrent (see [9]) 2-form of rank 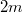 , two structure vector fields
, two structure vector fields 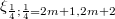 , two structure 1-forms
, two structure 1-forms 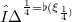
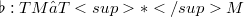 is the musical isomorphism [6] defined by g) and the pseudo-Riemannian tensor g of M respectively.
is the musical isomorphism [6] defined by g) and the pseudo-Riemannian tensor g of M respectively.DOI Code:
10.1285/i15900932v8n1p123
Full Text: PDF


