Saturated classes of bases
Abstract
In this paper we consider classes consisting of pairs 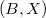 , where
, where 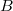 is a base of cardinality
is a base of cardinality 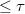 for the open subsets of a space
for the open subsets of a space  . Such classes are called classes of bases. For such a class
. Such classes are called classes of bases. For such a class  we define the notion of a universal element: an element
we define the notion of a universal element: an element 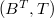 of
of 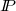 is said to be universal in
is said to be universal in 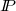 if for every
if for every 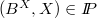 there exists an embedding
there exists an embedding 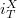 of
of  into
into 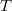 such that
such that 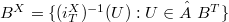 . We define also the notion of a (weakly) saturated class of bases similar to that of a saturated class of spaces in [2] and a saturated class of subsets in [3]. For the (weakly) saturated classes of bases we prove the universality property (that is, in any such class there exist universal elements) and the intersection property (that is, the intersection of not more than
. We define also the notion of a (weakly) saturated class of bases similar to that of a saturated class of spaces in [2] and a saturated class of subsets in [3]. For the (weakly) saturated classes of bases we prove the universality property (that is, in any such class there exist universal elements) and the intersection property (that is, the intersection of not more than  many saturated classes of bases is also saturated). We give some relations between these classes and the classes of spaces and classes of subsets. Furthermore, we give a method of construction of saturated classes of bases by saturated classes of subsets.
many saturated classes of bases is also saturated). We give some relations between these classes and the classes of spaces and classes of subsets. Furthermore, we give a method of construction of saturated classes of bases by saturated classes of subsets.
Also, we consider classes consisting of triads 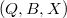 , where
, where 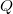 is a subset of a space
is a subset of a space  and
and 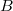 is a set of open subsets of
is a set of open subsets of  such that the set
such that the set 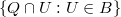 is a base for the open subsets of the subspace
is a base for the open subsets of the subspace 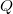 . Such classes are called classes of p-bases (positional bases). For such classes we also define the notion of a universal element and the notion of a saturated class of p-bases and prove the universality and the intersection properties. Some examples are given.
. Such classes are called classes of p-bases (positional bases). For such classes we also define the notion of a universal element and the notion of a saturated class of p-bases and prove the universality and the intersection properties. Some examples are given.
Full Text: PDF


