TheNeumann Laplacian on spaces of continuous functions
Abstract
If 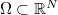 is an open set, one can always define the Laplacian with Neumann boundary conditions
is an open set, one can always define the Laplacian with Neumann boundary conditions 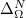 on
on 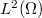 . It is a self-adjoint operator generating a
. It is a self-adjoint operator generating a 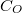 -semigroup on
-semigroup on 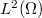 . Considering the part
. Considering the part 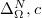 of
of 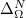 in
in 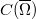 ,we ask under which conditions on it generates a
,we ask under which conditions on it generates a 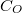 -semigroup.
-semigroup.
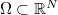 is an open set, one can always define the Laplacian with Neumann boundary conditions
is an open set, one can always define the Laplacian with Neumann boundary conditions 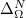 on
on 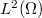 . It is a self-adjoint operator generating a
. It is a self-adjoint operator generating a 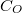 -semigroup on
-semigroup on 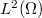 . Considering the part
. Considering the part 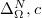 of
of 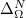 in
in 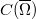 ,we ask under which conditions on it generates a
,we ask under which conditions on it generates a 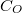 -semigroup.
-semigroup.DOI Code:
10.1285/i15900932v22n1p65
Keywords:
Neumann Laplace
Full Text: PDF


