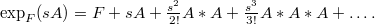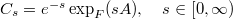Existence of limits of analytic one-parameter semigroups of copulas
Abstract
A 2-copula 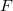 is idempotent if
is idempotent if 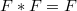 . Here
. Here  denotes the product defined in [1]. An idempotent copula
denotes the product defined in [1]. An idempotent copula 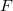 is said to be a unit for a 2-copula
is said to be a unit for a 2-copula 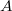 if
if 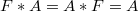 . An idempotent copula is said to annihilate a 2-copula
. An idempotent copula is said to annihilate a 2-copula 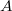 if
if 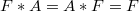 .
.
If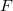 is a unit for
is a unit for 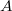 and
and  is a non-negative real number, define
is a non-negative real number, define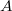 and any idempotent copula
and any idempotent copula 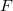 which is a unit for
which is a unit for 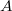 , the set
, the set operation, which is homomorphic to the semigroup
operation, which is homomorphic to the semigroup 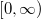 under addition. We call this set an analyticone-parameter semigroup of copulas.
under addition. We call this set an analyticone-parameter semigroup of copulas. 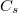 can be defined also for
can be defined also for  , and
, and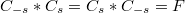 , but in general
, but in general 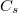 is not a copula for
is not a copula for  .
.
We show that for any such analytic one-parameter semigroup, the limit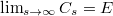 exists. We show also that the limit
exists. We show also that the limit 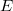 has the followingproperties:
has the followingproperties:
(i)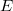 is idempotent.
is idempotent.
(ii)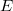 annihilates
annihilates 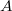 ,
, 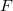 and
and 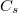 .
.
(iii)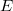 is the greatest annihilator of
is the greatest annihilator of 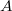 and of
and of 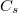 ,
, 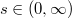 .
.
\noindent It is also true that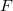 is the least unit for
is the least unit for 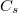 ,
,  . We give a geometrical interpretation of this result, and we comment on theuse of analytic semigroups to construct Markov processes with continuousparameter.
. We give a geometrical interpretation of this result, and we comment on theuse of analytic semigroups to construct Markov processes with continuousparameter.
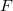 is idempotent if
is idempotent if 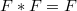 . Here
. Here  denotes the product defined in [1]. An idempotent copula
denotes the product defined in [1]. An idempotent copula 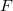 is said to be a unit for a 2-copula
is said to be a unit for a 2-copula 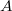 if
if 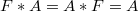 . An idempotent copula is said to annihilate a 2-copula
. An idempotent copula is said to annihilate a 2-copula 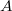 if
if 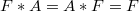 .
.If
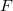 is a unit for
is a unit for 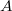 and
and  is a non-negative real number, define
is a non-negative real number, defineFor any copula
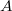 and any idempotent copula
and any idempotent copula 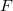 which is a unit for
which is a unit for 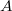 , the set
, the setis a semigroup of copulas under the
 operation, which is homomorphic to the semigroup
operation, which is homomorphic to the semigroup 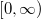 under addition. We call this set an analyticone-parameter semigroup of copulas.
under addition. We call this set an analyticone-parameter semigroup of copulas. 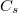 can be defined also for
can be defined also for  , and
, and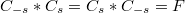 , but in general
, but in general 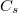 is not a copula for
is not a copula for  .
.We show that for any such analytic one-parameter semigroup, the limit
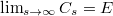 exists. We show also that the limit
exists. We show also that the limit 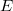 has the followingproperties:
has the followingproperties:(i)
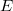 is idempotent.
is idempotent.(ii)
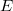 annihilates
annihilates 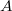 ,
, 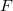 and
and 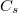 .
.(iii)
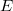 is the greatest annihilator of
is the greatest annihilator of 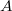 and of
and of 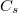 ,
, 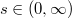 .
.\noindent It is also true that
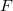 is the least unit for
is the least unit for 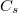 ,
,  . We give a geometrical interpretation of this result, and we comment on theuse of analytic semigroups to construct Markov processes with continuousparameter.
. We give a geometrical interpretation of this result, and we comment on theuse of analytic semigroups to construct Markov processes with continuousparameter.DOI Code:
10.1285/i15900932v30n2p1
Keywords:
copula; idempotent; star product
Full Text: PDF